在刚刚落幕的第63届国际数学奥林匹克竞赛中,中国再一次拿出了“独孤求败”的战绩:中国队6名参赛队员并列第一,全员摘金,且全部满分。
在网友们“中国人数学都好的洗脑包又加深了”的祝贺和调侃中,我们不禁也想问:中国人的数学,为何这么强?
《史记·留侯列传》中,记载了郦食其劝说刘邦封立六国、张良分析理由并加以阻止的场景,当刘邦兴致勃勃对张良讲述郦食其的观点时,张良答道:“臣请藉前箸为大王筹之。”随即用筷子充当算筹,为刘邦一一数出利弊,这一幕被称为“运筹借箸”。“运筹”原本指用算筹计算,衍生出经略谋划之意,“运筹帷幄之中,决胜千里之外”,就是刘邦后来对张良的评价。现代应用数学学科中的Operations Research引入中国时,也被译为“运筹学”。
在我国古代,数学通常被称为“算学”。算筹——形如筷子的小棍,是先人使用数千年的“计算器”,其运用法则蕴含着中国古代数学中基本的位值思想、表达形式和计算方法,影响不可谓不深远。尽管随着时间推移,算筹在元代以后逐渐淡出,但在它基础上衍生出的算盘和“苏州码”沿用至近现代。
算筹:演天地之数
算筹又名算子、筹策,它究竟在何时出现已不可考。《易经》记载:“上古结绳而治。”可以看作一种最原始的记录事件兼计数方式,其他古文明中亦有应用。在此基础上,先民逐渐研制出更便于使用的计算工具。

南美洲印加人曾用于记事的“奇普”(Quipu),是将多根打结的绳子系在同一根横向绳索的下方,不同形状的绳结可以代表不同数字,也可以用来计算总数,不同颜色则代表时间、物品等复杂信息
《史记·历书》记载:“黄帝使羲和占日,常仪占月,臾区占星气,伶伦造律吕,大桡作甲子,隶首作算数,容成综此六术而著调历。”虽然隶首为上古传说中的人物,但也可一窥“算数”历史之悠久,并且是为满足人民的实用需求而诞生的。
晋代人整理的《逸周书》中有“卑辞而不听,□财而无枝”之语,有研究者认为,“枝”指的是周代使用的算筹雏形。早期的算筹可能是使用取材方便的竹棒、树枝随意为之,“算”“筹”“策”等字都体现出它的质地。用来盛算筹的容器,叫做“中”,《周礼》中记载“凡射事,饰中,舍算”,后世有注“中,所以盛算也”,它很可能也是竹子制成的筒状容器。
在春秋时期,算筹的使用已经相当普遍,《论语》中有“斗筲之人,何足算也”,《老子》也提到“善计者不用筹策”。1954年,在湖南左家公山的楚国墓葬里出土了40根竹算筹,是目前已知最早的算筹实物。在《汉书·律历志》中,明确了它的制作规范:“其算,法用竹,径一分,长六寸,二百七十一枚而成六觚,为一握。”换算成今天常用的单位,就是直径约0.23厘米、长约13.8厘米的直棒,一套共271根,叫做“一握”,可以放在一个六边形的容器里。
古人常用的算筹除了竹制,亦有金属制、骨制、玉石制。横截面不仅有圆形,也有不易滚动的长方形。《晋书·王戎传》中,用“每自执牙筹,昼夜算计”描述王戎“积实聚钱”的勤奋程度。宋代《邵氏闻见后录》描写了略为灵异的一幕:“盗夜发咸阳原上古墓,有火光出,用剑击之,铿然以坠,视之,白玉帘也。岂至宝久埋藏欲飞去邪?既击碎之,有中官取以作算筹。”古人用帘,需能随意舒卷,因此白玉帘可能不是整片的白玉,而是由多条磨细的玉棒连缀而成,正适合做算筹。


骨制算筹、铅制算筹
古人为了携带方便,通常将算筹放在一个布袋里,挂在腰带上,这个布袋亦名“算袋”。《旧唐书·舆服志》规定,“一品以下文官并带手巾算袋”。连海中的乌贼也因为外形略似有飘带的袋子,被古人认为“秦皇东游,弃算袋于海,化为此鱼”。

我国胶州湾以南的海域有一种珊瑚纲无脊椎动物沙箸海鳃(Virgularia sp.),因为躯干主体部位呈细长笔直的圆柱形,很像一根算筹,古人称之为“越王余算”,并创造了相关传说:“昔晋安越王渡南海,将黑角白骨作算筹,其有馀者,弃于水中而生此,故叶白者似骨,黑者似角。”
纵横布筹,算无遗策
算筹应当如何表达数字和做计算?或许有人会联想起一个经典的笑话:老师教学生写字,讲“‘一’字画一横,‘二’字画两横,‘三’字画三横”,学生马上觉得自己都学会了。父亲让他给姓“万”的人写封信,他画了一天还没画完道道。
看上去像一根根小棍的算筹,要怎么表达数字呢?难道也像这个故事里的学生那样,表达数字“一”摆一根,数字“十”摆十根,数字“万”摆一万根吗?其实,古代的算筹记数依据是“位值制”记数法,即每个数字所表达的数值不仅取决于它本身,而取决于它在记数中所处的位置,这样就能够用较少的符号表达较大的数。算筹的位值制记数法建立在十进制基础上,即每满十数进位,相比于二十进制、六十进制,这种进位制的应用最广泛,我们今天使用的运算法则也是基于十进制的。
至迟在春秋时期,我国的十进位值制已经成熟。《墨子·经下》中提到:“一少于二,而多于五,说在建。”意思是,如果一和二都位于个位,一比二小;但如果一位于十位及以上,它代表的数字就比位于个位的五大。《左传·襄公三十年》记载,晋国绛县老人自称“臣生之岁,正月甲子朔,四百有四十五甲子矣,其季于今,三之一也”。意思是他出生以来经历了445个甲子日,最后一个甲子日是20天前。官吏询问大臣他应该有多少岁,师旷说:“73年。”史赵则给出了一个字谜:“亥有二首六身,下二如身,是其日数也。”答案也是73年。“亥”字的篆体上有二横,下面是三个“人”字,形同“六”字,如果把上面的“二”移到下方,就成了“二六六六零”,将天数折合为年就是73年。(如果是2666天,和现实不符)
约成书于公元3世纪前的《孙子算经》记载了基本的算筹记数法则:“凡算之法,先识其位。一纵十横,百立千僵,千十相望,万百相当。”
“一纵十横,百立千僵”直观地说明了算筹采用的纵式和横式两种记数方法,个位用纵式,十位用横式,百位再用纵式……这样相邻数位纵横交替摆放,避免数位太多时发生混淆。从1到5的数字可以直接摆放对数目的算筹,如果要用算筹表达从6到9的数字,则不需要摆和数字一样多的根数,而是先摆一根代表5,再在和它垂直交叉的方向放上1到4根,就可以分别代表从6到9的数字。算筹中没有表达“零”的字符,用空位代替0。《夏侯阳算经》概括为“满六已上,五在上方,六不积算,五不单张”。
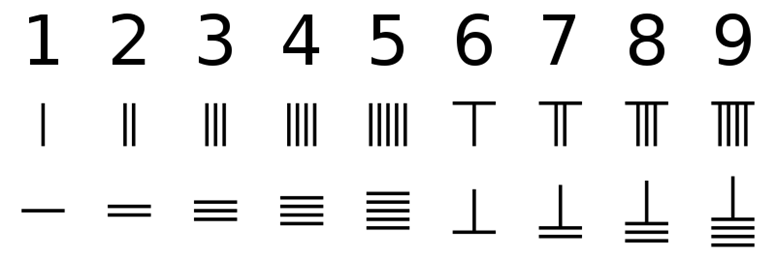
算筹摆位的时候,高位在左,低位在右,和现代的阿拉伯数字相同。如果要摆数字“71824”,并不需要摆71824根,只需要在个位摆4根,十位摆2根,百位摆8根,千位摆1根,万位摆7根就可以。因此,现代认为,“算筹系统是世界上唯一只用一个符号的组合,表示任何十进位数字的系统”。

永乐大典算筹布位
与之相比,其他古文明中的记数法则显得较为繁琐。比如,以古埃及的数字形式表达“3244”,需要写3个表达1000的文字、2个表达100的文字、4个表达10的文字和4个表达1的文字,并且外形各不相同。古希腊数字则是用不同的字母表达从1到9的数、10到90的十位数和从100到900的百位数,在书写数字时,将对应的字母写在一起,如写“241”就是将代表200的σ、代表40的μ和代表1的α三个字母并列。如果数字较大,则不利于计算和记录得数。


石刻上左栏中间表达数字为2,中下为2/3,底部为1/12;中栏中间表达数字为60,右栏顶部为1/30,中间为1/40
用算筹做加法、减法,是按照从左到右的顺序,从高位到低位逐位相加、相减,随着加减的结果及时摆出对应位上的算筹,也可以直接在被加或被减的数字上操作,把每位数的结果摆成新的。乘除法也类似,以乘法为例,古人的做法是“上下相乘,实居中央”,先把乘数和被乘数按上下位置摆好,按从左到右的顺序用上面的数的第一位乘下面数的每一位,把乘得的积摆在上下两数中间,然后去掉上面的数的第一位,把下面的数往右移动一位;再用上面数的第二位乘下面数的每一位,把结果和中间的乘积相加……这样以此类推,直到计算完成。做除法是将被除数放中排,除数放下排,商数放上排,余数放在最下一排,刘徽《九章算术注》中定义,在上的筹称“实”,在下的筹称为“法”。
如果用算筹做涉及负数的计算,可以将算筹涂上不同的颜色,宋代使用红色的算筹表示正数、黑色的表示负数;如果使用同色算筹,就在数字最后一位斜放一根,以示区分。做小数计算的话,要将小数部分和整数部分区分开,南宋秦九韶采用的方式是在个位数下记单位名称,比如要计算天数,就在个位数下面标一“日”字。元代刘瑾则将小数部分整体下移一格。做分数计算时,和现代的分数表达形式一样上下摆放,《孙子算经》称在上的筹为“子”,在下的筹为“母”,这就是“分子”“分母”的由来。

《仙筹增庆图》,托名南宋李嵩,绘神山海屋列仙对坐,童子搬筒筹开算
算筹能够将每一步的计算结果清晰地表达出来,甚至连视力有障碍的人也能熟练运用它做计算,《梦溪笔谈》里记载了一位擅长算筹的盲人卫朴,“大乘除皆不下照位,运筹如飞,人眼不能逐。人有故移其一算者,朴自上至下手循一遍,至移算处,则检正而去”。体现出中国传统数学解决问题的“机械化”特点,即每一步骤都具有固定程序。除了四则运算,算筹还可以用来做开方、开立方,解高次方程、四元方程等,自先秦至宋代的诸多领先当时世界的数学成就,都离不开算筹的助力。作为我国古代数学的基石,它在推演历法、修建工程、计算人口和赋税等方面都发挥了重要作用。
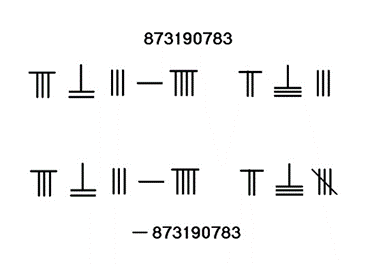

算筹表达正负数、分数方式
从算筹到算盘:形改法不变
算筹虽然计算迅速、表意清楚,但它仍然有使用不便之处,最大的问题在于用算筹做计算时,需要“铺摊子”,占地面积较大。自唐代以来,人们不再“席地而坐”,几案上要容纳大量的算筹并不容易。唐代尚书杨损有一次考察两个小吏的计算速度,“令俯阶筹之,且曰先达者胜”,就是在台阶上就地摆开算筹计算,说明要计算的数字较为复杂。如果算筹摆得较多,很容易受到外界干扰而弄乱,从而影响结果。
西岳华山有一处名为“芦花池”的景点,相传后魏道士寇谦之曾在这里修炼,“定天元五纪,其算有差,后成公与真人佯狂而来,假为货客误触算筹,其算乃合”,寇谦之便追随真人而去,剩下的算筹留在池边,变成了丛丛芦苇。唐代以后,随着商业的发展,民间对“便携式”计算工具的需求更为迫切。

算盘
关于算盘的起源时间,竟有自汉代到元代多种不同的说法,跨度约一千年。汉代《数术记遗》最早有“珠算,控带四时,经纬三才”的记载,但没有说明珠算工具的形制。北周甄鸾注(一说该书为甄鸾伪托前人所作):“刻板为三分,其上下二分以停游珠,中间一分以定算位。位各五珠,上一珠与下四珠色别。其上别色之珠当五。其下四珠,珠各当一。至下四珠所领,故云控带四时。其珠游于三方之中,故云经纬三才也。”从中可以看出,甄鸾所记载的运算工具,更像是将算筹直接替换成算珠,放在有刻度的专用板子上使用,还没有后来以柱穿珠、设置横梁的造型,但也可以认为是算盘的一种雏形。
在漫长的岁月中,算盘不断发生演变,最终固定为最适宜人们使用的形式。实际上,算盘的数字表达形式和基本运算法则都是在算筹的基础上发展出来的,只是把细长的算筹变成了适宜操作的珠子,并且让它们不能随意移动。最明显的特点就是横梁上半部每个算珠代表5,下半部每个算珠代表1,“珠动则数出”,正符合算筹“五不单张”的法则,并且算盘计算也是从高位到低位。

《清明上河图》局部
在艺术作品中最早出现的算盘来自宋代《清明上河图》,画中的“赵太丞家”药店柜台上,有一个长方形物体,隐约可见上面有15串珠子。能够形成佐证的是,明代程大位《直指算法统宗》中收录的算书名录中包括宋代《盘珠集》《走珠集》,从名称看,可能是介绍算盘使用方法的算书,但这两本书均已失传。宋代《南部新书》中记载,“近有钟离令王仁岫,善工算……但用诸法径门,取其简要,若类鼓珠之法”,学界认为“鼓珠”可能指的是算盘珠。另一方面,宋代的计算口诀进一步完善,如《梦溪笔谈》记录了“欲九除者增一,八除者增二”的“增乘法”,演变为“归除法”,在珠算中一直沿用。可以看出,宋代是算盘发展的一个重要转折阶段,这与宋代商业社会的繁荣必然相关。
元代陶宗仪的《南村辍耕录》中,将仆人比喻成“三珠”,成为流传一时的经典比喻:“凡纳婢仆,初来时曰擂盘珠,言不拨自动;稍久,曰算盘珠,言拨之则动;既久,曰佛顶珠,言终日凝然,虽拨亦不动。”可见在当时算盘已经是常见之物。明初《鲁班木经》中最早记载了算盘的规格:“一尺二寸长,四寸二分大。框六分厚,九分大,起碗底线。上二子,一寸一分;下五子,三寸一分”。随郑和下过三次西洋的通事马欢著有《瀛涯胜览》,其中介绍“古里国”(今印度南部喀拉拉邦科泽科德市)时写到:“彼之算法无算盘,但以两手并两脚十指计算”,也表明了算盘在明代的普及程度。

明代徐心鲁著《盘珠算法》,介绍珠算口诀和应用题等,是现存最早绘有算盘图的珠算书。图中所绘的明式算盘是上一珠、下五珠,用黑珠和白珠分别演示运算中的“动珠”与“静珠”。明代后期开始出现上二珠、下五珠的算盘形式,这和当时使用“一斤十六两”的度量衡有关
算盘出现以后,算筹仍然与之并行使用了一段时间。明初有一本图文对照蒙童读物《魁本对相四言杂字》,类似于现代的“看图识字”,其中列出的名词里,既有算盘,又有算子(算筹),可见这两者对当时的人来说都不陌生。到了万历年间,有个叫何孚可的人以“弘雅博物”著称,“每出入,必以算筹随”,侧面体现出当时算筹已经是一种不常见的古物,随身携带它成了值得一记的轶事。
与算筹的没落形成对照的是算盘的迅速发展,多种介绍珠算算法的著作广为传播,琅琅上口的计算口诀令它学习起来更容易、计算速度更高效。自明代至现代,算盘作为最主要的计算工具,在各行各业应用了五百多年,直到被电子计算器全面取代。

明代程大位著《直指算法统宗》又名《算法统宗》,共十七卷,汇总介绍珠算算法与应用题解法,流传极广,“海内握算持筹之士,莫不家藏一编”,并传入日本、朝鲜、东南亚地区
中国古代的计算工具,体现出的是我国古代数学一脉相承的机械化思想,以解决现实生活中的各类问题为主要目的。在这一思想引领下,明清时期我国基础计算水平发展到高峰,但不能否认的是在一定程度上造成了数学发展的局限。
今天,人们已经习惯使用电脑或电子计算器,算筹和算盘都成为了历史名词,但并没有彻底从我们的生活里消逝。
【免责声明】上游新闻客户端未标有“来源:上游新闻”或“上游新闻LOGO、水印的文字、图片、音频、视频”等稿件均为转载稿。如转载稿涉及版权等问题,请联系上游。